Chapter 4 A deeper understanding of Options
This chapter aims at digging a bit more into European options and the model used to price them: the Black-Scholes model.
I have asked myself a lot of questions about the following chapters, trying to figure out where to start and how deep into mathematics should I go?
My goal is to get you to have the best understanding of options as possible. Mathematics is not always useful and necessary as you can get a great sense of options with a good intuition. I mainly rely on intuition when teaching this material.
As it might help the more quantitative profiles among the readers to dig into the mathematics behind the Black-Scholes model, I decided to share the derivation of the Black-Scholes Equation in Appendix of this chapter. For the others, there is surely enough maths in this chapter anyway.
4.1 The Black-Scholes model
Black and Scholes developed a closed-form pricing formula for European options. The market assumptions behind their model are quite strong and contained:
- Constant volatility
- Constant interest rates
- Log-normality distributed stock prices
- Constant dividend yield
The concept of risk-neutral pricing is at the heart of the Black-Scholes model.
4.1.1 Risk-Neutral Pricing
In finance, when pricing an asset, a common technique is to discount the expected cashflows. The expected cashflows are calculated using the real-world probability of each cashflow and the risk adjustment takes the form of a higher discount rate.
In the theory of risk-neutral pricing, the real-world probabilities assigned to future cash flows are irrelevant, and we must obtain what are known as risk-neutral probabilities.
The fundamental assumption behind risk-neutral valuation is to use a replicating portfolio of assets with known prices to remove any risk. By the no-arbitrage condition, we can create a pricing model by setting the temporary risk-less hedged portfolio return to the risk-free rate instead of unknown market expectations. The amounts of assets needed to hedge determine the risk-neutral probabilities.
Under the aforementioned assumptions, the Black–Scholes theory considers options to be redundant in the sense that one can replicate the payoff of a European option on a stock using the stock itself and risk-free bonds.
As such, the key feature of the Black–Scholes framework is that it is preference-free: since options can be replicated, their theoretical values do not depend upon investors’ risk preferences, only upon the current stock price and its dynamics.
Therefore, an option can be valued as though the return on the underlying is riskless. This risk-neutral assumption behind the Black–Scholes model constitutes a great advantage in a trading environment. In the risk-neutral world, all cashflows can be discounted using the risk-free rate (r) whereas, in a real word, the discount rate should take into account the risk premium, which is more delicate.
A small example
Let me share with you a nice practical example that might help you to grasp the concept of risk-neutral valuation.
Suppose a first horse has 20% chance to win while a second horse has 80% chance to win.
\(10.000€\) is bet on the first horse and \(50.000€\) is bet on the second.
If odds are set to 4:1, then:
- The bookmaker may gain \(10.000€\) if the first horse wins \((50.000€ - 4*10.000€)\).
- The bookmaker may loose \(2500€\) if the second horse wins \((10.000€ - 1/4*50.000€)\).
- The bookmaker’s expected profit is 0 \((0.2*10.000€ + 0.8*-2500€)\).
If odds are now set to 5:1, then the bookmaker won’t lose or gain money no matter which horse wins. That represents the risk-neutral probabilities.
4.2 European Call Options
4.2.1 Introduction
A call option is a financial contract that gives its holder the right, but not the obligation, to buy a specified amount (nominal = N) of an underlying asset (S) at a specified price (strike price = K) within a specific time period (maturity = T).
Therefore, a call buyer profits when the underlying asset increases in price.
It is important to distinguish between payoff at maturity, premium or market price and profit.
4.2.2 Buyer’s payoff at maturity
\(\boxed{C_T = Max(S_T \; - \; K, 0) = (S_T \; - \; K)^+ = \; 1_{\{ S_T > K \}} (S_T \; - \; K) }\)
It is good that you get familiar with these notations as soon as possible as you will see them a lot through this material. You must know them perfectly when working in equity derivatives.
\(1_{S_T>K}\) is an indicator function having a value of 1 if \(S_T\) > K and 0 otherwise.
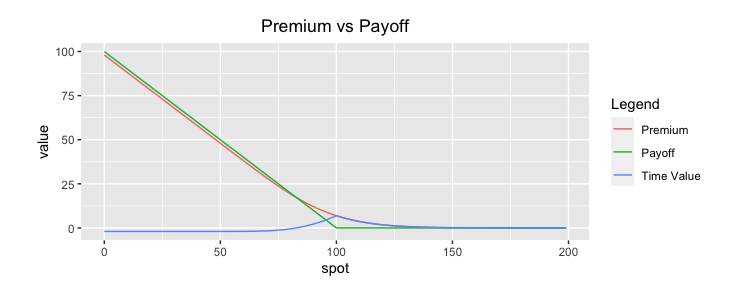
Let’s plot the Call payoff with respect to the underlying spot price.
Fig: 4.1 : Call Payoff at Maturity
As you can see in the graph, the option’s strike price is the key point which divides the payoff function in two parts. Below the strike, the payoff chart is constant and null.
Above the strike the line is upward sloping, as the call option’s payoff is rising in proportion with the underlying price.
So you have got nothing to lose at maturity when buying a call option. you will therefore have to pay for this right!
How much?
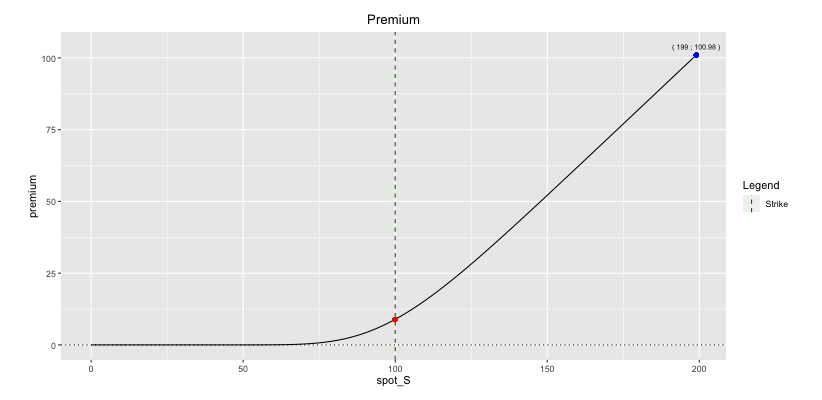
Well, that’s given by the call option premium and we will see now how to calculate it.
The good thing when buying a call option is that your loss is always limited to the premium paid for being long the call option. Inversely, when selling a call option, your potential loss is illimited.
The good thing with a long call trade is that your loss is always limited to the initial cost.
4.2.3 Market Price or Premium
The market price of the call option is called the premium. It is the price paid for the rights that the call option provides.
Option premiums are expressed as a per-share basis while most option contracts represent 100 shares of the underlying stock. Thus, a premium quoted as \(1.1€\) means that it will cost you \(110€\) as the option is generally on 100 shares.
4.2.3.1 Black-Scholes formula
The Call payoff at maturity is quite easy to understand but it does not tell you how much is the option worth at any time before expiry.
European Call Price: \(\boxed{C = Se^{-qt}N(d_1) \; – Ke^{-rt}N(d_2)}\)
Where
\(d_1 = \frac{\text{ln} \left(\frac{S}{K}\right) + \left(r \; - \; q \: + \: \frac{\sigma^2}{2}\right)t}{\sigma \sqrt t}\) and \(d_2 = \frac{\text{ln} \left(\frac{S}{K}\right) + \left(r \; - \; q \: - \: \frac{\sigma^2}{2}\right)t}{\sigma \sqrt t} = d_1 - \sigma \sqrt t\)
\(N(x) = \frac{1}{\sqrt{2\pi}} \displaystyle\int_{- \infty}^{x}{e^{-z^2/2}dz}\)
While all these equations might look scary at first. They reflect nothing but very intuitive concepts that can be understood by anyone out there.
A first observation is that the expected rate of return of the underlying S, μ, does not enter into those equations. In fact, the relevant parameter is the risk-free rate of interest. That is due to the risk-neutral assumption behind the Black-Scholes model.
Formula for both Calls and Puts can be split into two components that have a very intuitive meaning that will surely help you understand it better. Note that we assume the dividend yield, q, to be zero in the following development.
We have seen that Call option payoff at maturity is: \(\boxed{C_T = Max(S_T \; – \; K, 0) = (S_T \; – \; K)^+ = \; 1_{\{ S_T > K \}} (S_T \; – \; K)}\)
So, let us split this formula into two components so that: \(\boxed{C_T = C^1_T \ + \ C^2_T}\) and therefore \(\boxed{C_0 = C^1_0 \ + \ C^2_0}\) by the no-arbitrage argument.
The first component is the payment of the strike price, conditional on the option finishing in the money (= conditional strike payment).
The payoff of this claim is: \(\boxed{C^1_T = -K \ * \ 1_{\{ S_T > K \}}}\)
The second component is the receipt of the stock, conditional on the option finishing in the money (= conditional receipt of the stock).
Its payoff is: \(\boxed{C^2_T = S_T \ * \ 1_{\{ S_T > K \}}}\)
The Call option can therefore be valued by valuing each of these two components separately.
The present value of the conditional strike payment will be the expected future payment, computed on the basis of the risk-adjusted probability distribution, discounted at the risk-free rate.
The expected future payoff is: \(\boxed{E(C^1_T) = -K \ * \ P\{ S_T > K \}}\) where P is the risk-adjusted probability.
The present value is: \(\boxed{C^1_0 = -K*e^{-rT} \ * \ P\{ S_T > K \}}\)
It turns out that the risk-adjusted probability of the option finishing in the money is nothing but \(N(d_2)\): \(\boxed{P\{ S_T > K \} = N(d_2)}\).
Therefore, the present value of the conditional strike payment is: \(\boxed{C^1_0 = -K \ e^{-rT} \ N(d_2)}\)
Don’t you recognize part of the Call price formula?
The present value of the conditional receipt of the stock will also equal the expected future value of the stock, computed using the adjusted probabilities, discounted at the risk-free rate.
The expected future payoff of this component is the conditional expectation of the stock price given that option is exercised times the probability of the option being exercised: \(\boxed{E(C^2_T) = E[S_T | S_T > K] \ P\{ S_T > K \}}\)
This expression looks slightly more complicated than for the first component. This is simply due to the fact that the strike price K is a constant (and the expected value of a constant is nothing but the constant itself as it is known with certainty) while the stock price is a random variable.
It turns out that: \(\boxed{E(C^2_T) = E[S_T | S_T > K] \ P\{ S_T > K \} = e^{rT} S \ N(d_1)}\)
Therefore, the present value of the conditional receipt of the stock is: \(\boxed{C^2_0 = S \ N(d_1)}\)
Don’t you recognize part of the Call price formula?
By putting together the values of the two components of the option payoff, we get back to the Black-Scholes formula.
Why is the PV of the conditional receipt of the stock not \(S \ N(d_2)\), corresponding to an expected FV of \(e^{rT} S \ N(d_2)\) ?
Well, if it was the case the PV of the call option would be \((S \ – \ e^{-rT}K) \ N(d_2)\). This would be negative when the call option is OTM, which obviously cannot be the case.
Where is the flaw in the argument then?
It is that the event of exercising your option is not independent of the random magnitude of \(S_T\). If exercise were completely random and unrelated to the stock price, then indeed it would have been the case. However, exercise is not purely random and depends on the future stock price since it happens only when \(S_T\) is high.
Therefore, \(S e^{rT}N(d_2)\) underestimates the expected value.
\(\boxed{E[S_T | S_T > K] \ P\{S_T > K \} = E[S_T | S_T > K] \ N(d_2) > e^{rT} S \ N(d_2)}\)
because the correlation between \(S_T\) and the decision of exercising the call option implies that: \(\boxed{E[S_T | S_T > K] > e^{rT} S}\)
4.2.3.2 Numerical Application
In the absence of interest rates and dividends, the price of an ATM call can be approximated by the following formula: \(C_T = 0.4 \; \sigma \sqrt{T} \; S_0\)
4.2.3.3 Premium Graph
Plotting the Call price with respect to the spot price shows an ascending convex curve.
Fig: 4.2 : Initial Call Price for different Spot levels
Ascending curve: long call ⇒ positive delta ⇒ long forward.
Convex curve: long call ⇒ positive gamma.
4.2.3.4 Moneyness
Moneyness is a term describing the relationship between the strike price of an option and the current trading price of its underlying security.
Call options are said to be:
- In-the-money (ITM) if Spot price > Strike price.
- At-the-money (ATM) if Spot price = Strike price.
- Out-of-the-money (OTM) if Spot price < Strike price.
It is also time to bring up the concept of intrinsic value, which is the value any given option would have if it were exercised today. Plotting the intrinsic value yields the same graph as the payoff at maturity.
4.2.3.5 Comparison: Premium vs Payoff
Fig: 4.3 : Comparison: Premium vs Payoff
As we can see, the call price (red) is always bigger than the intrinsic value (green) of the option. The difference is the time value (blue), which measures the uncertainty of the option ending in-the-money (ITM). It is almost always positive for a call and reaches its maximum at-the-money (ATM). As time to maturity decreases, the time value decreases to be equal to zero at expiry date. In other words, Call options tend to lose some of their value as time passes (ceteris paribus). They usually loses around two-thirds of their time value during the last third of their life.
Do not worry if you are not familiar with some terms, we will see them in more details soon.
4.3 European Put Options
4.3.1 Introduction
A put option is a financial contract that give its holder the right, but not the obligation, to sell a specified amount (nominal = N) of an underlying asset (= S) at a specified price (strike price = K) within a specific time period (maturity = T).
Therefore, a put buyer profits when the underlying asset decreases in price.
It is important to distinguish between payoff at maturity, premium or market price and profit.
4.3.2 Buyer’s payoff at maturity
\(\boxed{P_T = Max(K \; - \; S_T, 0) = (K \; - \; S_T)^+ = \; 1_{\{ S_T < K \}} (K \; - \; S_T) }\)
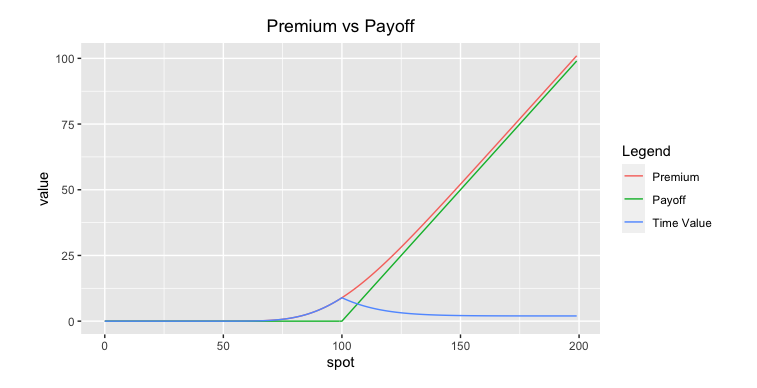
Let’s plot the Put payoff with respect to the underlying spot price.
Fig: 4.4 : Put Payoff at Maturity
As you can see in the graph, the option’s strike price is the key point which divides the payoff function in two parts. Below the strike, the payoff chart is in the positive territory and the payoff increases as the underlying price goes down. This relationship is linear.
Above the strike, the payoff is constant and null.
So you have got nothing to lose at maturity when buying a put option. you will therefore have to pay for this right!
How much?
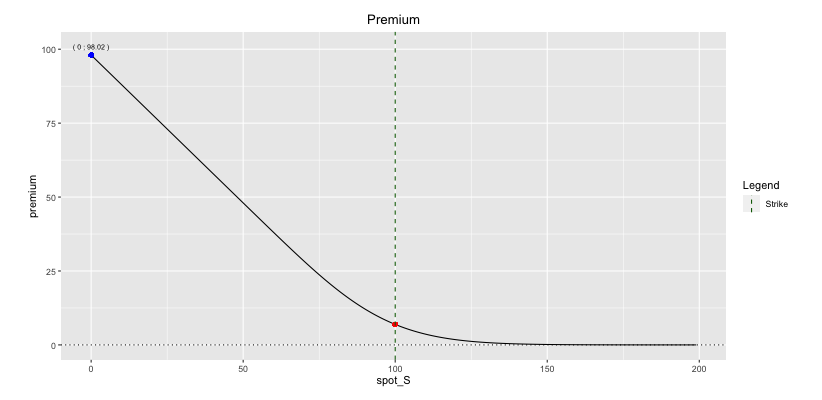
Well, that’s given by the put option premium and we will see now how to calculate it.
The good thing when buying a put option is that your loss is always limited to the premium paid for being long the put option. Inversely, when selling a put option, your potential loss can be quite substantial if the underlying stock price plunges.
4.3.3 Market Price or Premium
The market price of the put option is called the premium. It is the price paid for the rights that the put option provides.
Option premiums are expressed as a per-share basis while most option contracts represent 100 shares of the underlying stock. Thus, a premium quoted as \(1.1€\) means that it will cost you \(110€\) as the option is generally on 100 shares.
4.3.3.1 Black-Scholes formula
The Put payoff at maturity is quite easy to understand but it does not tell you how much is the option worth at any time before expiry.
European Put Price: \(\boxed{P = Ke^{-rt}N(-d_2) \: - Se^{-qt}N(-d1)}\)
Where
\(d_1 = \frac{\text{ln} \left(\frac{S}{K}\right) + \left(r \; - \; q \: + \: \frac{\sigma^2}{2}t\right)}{\sigma \sqrt t}\) and \(d_2 = \frac{\text{ln} \left(\frac{S}{K}\right) + \left(r \; - \; q \: - \: \frac{\sigma^2}{2}t\right)}{\sigma \sqrt t} = d_1 - \sigma \sqrt t\)
\(N(x) = \frac{1}{\sqrt{2\pi}} \displaystyle\int_{- \infty}^{x}{e^{-z^2/2}dz}\)
I am not going to develop this formula further as the idea behind it follows the same line of thought as for the Call option.
4.3.3.2 Premium Graph
Plotting the Put price with respect to the spot price shows a descending convex curve.
Descending curve: long put ⇒ negative delta ⇒ short forward.
Convex curve: long put ⇒ positive gamma.
4.4 Intrinsic Value and Time Value
4.4.1 Introduction
The concept of time value is very simple and intricate at the same time.
The time value can be defined as the value of the option above the intrinsic value. You should know by now that the intrinsic value is the value any given option would have if it were exercised today.
You can always express an option price as the sum of its intrinsic value and its time value.
\(\boxed{Option \; Price = Intrinsic \; Value + Time \; Value}\)
Call Intrinsic Value = Max(0; S - K)
Put Intrinsic Value = Max(0; K – S)
At first sight, one might assume that time value has to be a positive number. Well, if we take out-of-the money options, their intrinsic values are zero but their prices are typically not zero. Therefore, this differential is positive. Hence, we intuitively expect the time value to be positive.
While it is most often positive, we have seen that it could also be negative in some situations.
We will now discuss the attitude of time on call and put options.
4.4.2 Time Value of Call Options
Let us prove the positive attitude of the time on a call option by considering both OTM and ITM cases.
4.4.2.1 OTM and ATM Cases
OTM and ATM cases are trivial since premium is always positive and hence always more than the intrinsic value being worthless.
4.4.2.2 ITM Case
Suppose we own an in-the-money European call and want to lock the intrinsic value \(S_0 - K\). We can do it by selling forward the stock to freeze the price risk.
If the option ends up in-the-money, we will exercise the option and our cashflow will be: \(\boxed{S_0e^{(r \; - \; q)T} \; - \; K}\)
If the option ends up out-of-the-money, we won’t exercise it and the only cashflow will be: \(\boxed{S_0e^{(r \; - \; q) T} \; - S_T > S_0 e^{(r \; - \; q)T} \; - K}\)
If \(S_0e^{(r \; - \; q)T} \; - K\) is always bigger than the intrinsic value \(S_0 - K\), then the cost of this hedge (= the call price) needs to be above this final guaranteed outcome (by the no-arbitrage argument) \(\Rightarrow\) \(\boxed{Call \; price > S_0-K}\). In such cases, the time value will always be positive.
On the contrary, if this inequality is not always verified, time value can happen to be negative.
4.4.2.3 Conclusion
The time value of a Call option is always positive except for deep ITM calls when (r - q) is negative. This is the case when the dividend yield of the underlying stock is higher than the risk-free interest rate (q > r). Note that this includes the case of a non-dividend paying stock in a negative interest-rate world.
The always positive time value of Call options on non-dividend paying stocks in a positive rates environment explains why there is no difference in premium between American and European Calls on such underlyings.
4.4.3 Time Value of Put Options
We can wonder why this argument does not hold for put options. It looks reasonable to do the same thing.
4.4.3.1 OTM and ATM Cases
OTM and ATM cases are trivial since premium is always positive and hence always more than the intrinsic value being worthless.
4.4.3.2 ITM Case
For hedging in-the-money put options, we need to buy forward the stock to freeze the price risk and lock the intrinsic value \(K - S_0\).
If option ends up ITM, we will exercise the option and our cashflow will be: \(\boxed{K \; - \; S_0e^{(r \; - \; q) T}}\)
If option ends OTM, we won’t exercise and our cashflow will be: \(\boxed{S_T \; - \; S_0 e^{(r \; - \; q) T} \; > \; K \; - \; S_0 e^{(r \; - \; q) T}}\)
By the no-arbitrage argument, the cost of this hedge needs to be above this final guaranteed outcome. \(\Rightarrow\) \(\boxed{Put \; price > K-S_0 \; e^{(r \; - \; q)T}}\)
However, since \(\boxed{ K \; - \; S_0 e^{(r \; - \; q)T} \; < \; K - S_0}\) when interest rate is bigger than the dividend yield of the underlying stock, it becomes possible that the premium is less than the intrinsic value and therefore the time value negative.
4.4.3.3 Conclusion
The time value of a Put option is always positive except for deep ITM Puts when the interest rate is bigger than the dividend yield (r > q). This happens more frequently as some stocks do not pay dividends. That was the case in Fig: 3.6 where I plot a 1-year put option on a non-dividend paying stock in a 2% interest-rate world.
So the situations where the time value is negative can be traced back to the cashflows. Receiving money now or receiving the same amount of money in the future is not the same. And the direction of the cashflows in case of the put option are reversed!
The whole construction here is a nice example of proxy hedging the option.
However, the outcome of the hedging strategy is unsure. We had inequalities rather than equalities.
The reason for the residual risk has to do with the fundamental aspect of options.
We started by saying that the option was ITM and hedging accordingly. If then, afterwards, it turns out to be OTM, there arises a risk/uncertainty in the value the hedge will produce. The balance between the option and the hedge is broken at that time.
4.5 The Cost of Hedging
I will never emphasize it enough but it is very important to remember that the price of an option should reflect the cost of hedging it!
There are many parameters to consider when pricing an option: interest rates, volatility, repo, dividends, exchange rate, correlation, etc.
For european options, these parameters can be inserted into the Black-Scholes formula to get their prices. Such closed-form solutions that reflect the cost of hedging do not always exist for more sophisticated payoffs. Moving towards more complicated options, it is essential that you keep in mind that the cost of an option should reflect the cost of hedging the risks entailed!
Often all the risks are not hedgeable so that the product won’t be fully hedged to replication. It will then be hedged so that the remaining risk exposures are tolerable according to the risk department.
Pricing an exotic product therefore comes down to understand, manage and price the underlying risks.
4.6 The Call-Put Parity
4.6.1 Introduction
Put–call parity specifies a relationship between the prices of european call and put options with the identical strike price K and expiry T. Perhaps the most important feature of put–call parity is that it must be satisfied at all times, in a model independent manner. A violation of this leads to arbitrage opportunities.
4.6.2 The Call-Put relationship
\(\boxed{Call(K,T) - Put(K,T) =S_0e^{-qT} - Ke^{-rT}}\)
The left side of this equality consists of a portfolio A, which is a long call position and a short position with the same strike price and maturity (K,T) on the same underlying asset S.
The right side of this equality consists of a portfolio B, which is a long position in a forward contract that gives its holder the obligation to buy the underlying asset A at a price K at maturity T. In all states, both portfolio A and B have the same payoff at maturity.
As early exercise is not possible for European options, if the values of these two portfolios are the same at the expiry of the options, then the present values of these portfolios must also be the same. If it is not the case, an investor can arbitrage and make a risk-free profit by purchasing the less expensive portfolio, selling the more expensive one and holding the long-short position to maturity.
Accordingly, we have the following price equalities:
\(\boxed{Call(K,T) - Put(K,T) = Forward(K,T)}\)
and
\(\boxed{Forward(K,T) = S_0e^{-qT} - Ke^{-rT}}\)
Fig: 4.7 : Call-Put Parity: Call - Put = Synthetic Forward